I have a t-shaped shelf bracket that looks like this:
| <- screw hole here
| <shelf>
|-----------
<wall>|
|
|
| <- screw hole here
This is a custom made bracket so there are no instructions. The wall side of the brackets can be oriented so there is 2" going up above the shelf and 4" down or the opposite where there's 4" above the shelf and 2" below.
What is the best orientation to minimize stress on the bolts?
Whether the 2" side up or the 4" side up, it doesn't matter in terms of the stress on the bolt.
We can do a simple analysis as below. In the figure below your T-shaped bracket in drawn in blue while the two bolts are drawn in red. For simplicity we assume that the bracket only contacts the wall via the two bolts at the very top and very bottom end. W is the total gravitational force of your bracket, shelf and its load. The forces on the two bolts are decomposed into perpendicular directions f1~f4.
Basic physics tells us that:
Therefore, the axial (horizontal) forces on the two bolts (f1 and f2) are equal and determined by the ratio of (2+4)/d, which is irrelevant to whether 2" or 4" is up or down. The vertical forces (f3 and f4) will add up to the total weight W, but their exact values are under-determined (but irrelevant to which side is up).
I am responding to Jim's questions in the comment.
(1) In my figure I clearly shows that f1 and f2 point in the opposite direction, therefore f1=f2. If you insist "use a consistent coordinate system" and "to the right is positive", then f1=-f2, but it doesn't change anything.
(2) Equation 3 is correct. Here we are calculating torque of W using bolt 1 as the origin (fulcrum). We are not calculating momentum or angular momentum. The torque of W is calculated as 
and obviously 
. That how to get equation 3. Or more generally,
BTW this is also why Willk's analysis based on "the longer the distance from fulcrum to end of the lever, the more the force is amplified" is wrong. Willk forgets about the angle between the force and lever arm.
Considering just a vertical vector parallel to the wall, I don't think it matters whether long side is on top or short side.
But there are other vectors. Consider the shelf like a lever. If you put a weight on the edge of the shelf it will want to pivot at the interface of shelf and wall, which will be the fulcrum of the lever. The edge of the shelf will want to rotate downwards and towards the wall. This will push the bottom of the bracket into the wall and the top of the bracket out of the wall.
Pushing the bottom into the wall is fine. Pulling the top away from the wall will stress the bolt at the interface with the wall, tending to pull it loose.
The longer the distance from fulcrum to end of the lever, the more the force is amplified. Having the long side on top will amplify forces levering the bolt out of the wall more than having the short side on top.
My answer: put the short side on top.
Also, if you have a relatively weak wall you could actually drive the entire bracket into the wall. The more surface area you have on the bottom, the more you distribute the force pushing the bracket into the wall. Another reason to put the long side on the bottom.
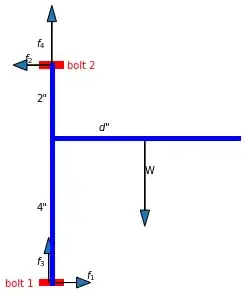
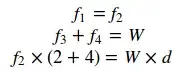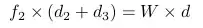EDIT I think the answer of @user12075 above is correct, that is, the pull-out force on the top screw is the same whether the shelf is installed with the longer vertical segment on top or the shorter vertical segment on top. The two lengths appear in the formula only as the sum, so if the two values are interchanged the result is the same. And that sum is in the denominator so the pull-out force is inversely proportional to the sum of the two.
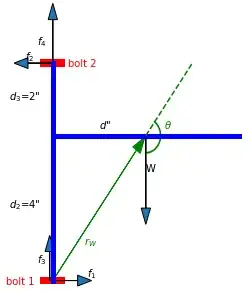
EDIT To explain my retraction of my original claim that that the longer vertical segment should be on top and my agreement with @user12075, one can use the intersection of the two parts of the Tee as the origin for calculating the three moments. That way each force of interest is perpendicular to its radius arm and so no trig is required.
Put the long side (4") on top. This gives a smaller pull-out force on the top screw than having the short side (2") on top.
Without doing calculations you can visualize how much the pull out force increases as the length of the top side would decrease toward zero. We all know that when using claw hammer to pull out a nail in a vertical wall by pulling down, it is easier as we get the nail deeper into the V of the claw. This means the pull-out force increases as the top side get shorter.
EDIT
I have to admit to being guilty of using vague intuition to answer the question, but I think there is no actual physical fulcrum at the position of the bottom screw. For example, if the vertical member is in uniform contact with the wall, then the wall is exerting force on the bracket all along its length.
One can modify the problem by doing away with the bottom screw. (The ELFA hanging shelves, standard installation has no bottom screw. ) Then all vertical force exerted on the bracket by the wall is exerted at the position of the top screw.
One can idealize the problem where the vertical member is in contact with the wall only at two points: the top screw and at the position of the bottom screw (which may or may not have a screw in it).
I installed a lot of ELFA hanging shelves in two houses which motivated me to do some figuring on the forces, but I have lost my calculations. I will see if I can redo it, but it would take a couple of hours of concentrated effort and I have a lot of distractions right now.
