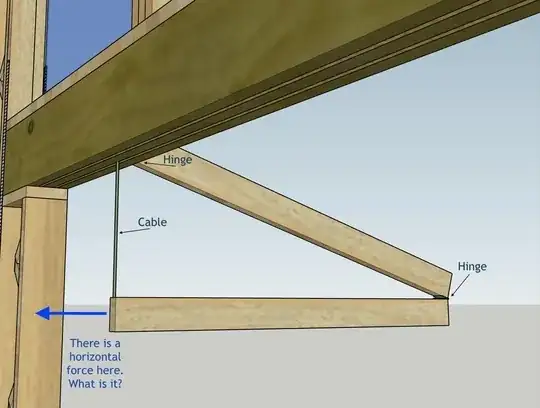
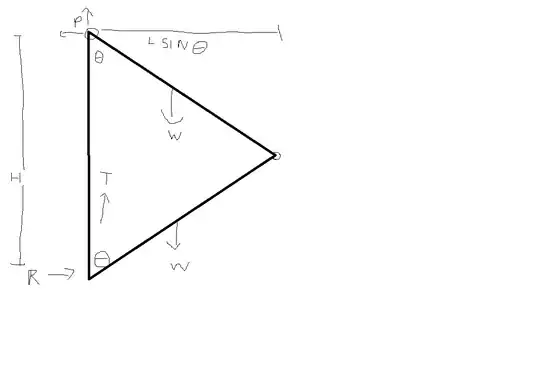
I am trying to calculate the horizontal force created by a raised hangar door, but for the purpose of this question, we can consider the horizontal force of a 2x4 stud that is connected as shown in the illustration below.
The 2x4 is cut in half and connected with a hinge at the top and a hinge at the middle, and then is supported vertically with a cable (which in the door will pull the door up and down). Not pictured is a track which the 2x4 or door will be connected to that keeps the "bottom" of the door in alignment with the opening.
What I am trying to determine is the method to find the lateral force that is created, or in other words, how much force will the door put on the track when it is open?
I have intentionally not included weights or lengths or angles because I'm looking for a general solution.