To determine the heat transfer rate (Q) of the open system in BTUs per hour, you can use the following formula:
Q (BTU/hr) = Flow Rate (GPM) x (Temperature Leaving Process (F) - Temperature Entering Process (F)) x 500.4
If the flow rate of the open system is 2.5 GPM, the temperature leaving the process is 105°F, and the temperature entering the process is 58.7°F, then the heat transfer rate can be calculated as follows:
Q = 2.5 GPM x (105°F - 58.7°F) x 500.4
= 2.5 GPM x 46.3°F x 500.4
= 59,526.85 BTU/hr
So the heat transfer rate in this case would be approximately 59,526.85 BTUs per hour.
A typical gas-fired 40 gallon water heater produces 34,000 BTUs per hour. The difference in the heat rates reduces the temperature in the 40 gallon tank. The difference equals 25,526.85 BTUs per hour, or 7.0907 BTU/sec.
To determine the value of dt (the change in time in seconds) using the formula:
dt = mcpdT/Q
Where m is the mass of the water in pounds, cp is the specific heat capacity of water (1 BTU/pound-F), dT is the change in temperature in degrees Fahrenheit, and Q is the heat transfer rate in BTUs per second, you will need to know the values of m, dT, and Q.
If m equals the mass of 40 gallons of water, the temperature change is 35 degrees Fahrenheit, and Q equals 7.0907 BTU/sec, then the value of dt can be calculated as follows:
dt = 40 gallons * 8.3454 pounds/gallon * 1 BTU/pound-F * 35°F / 7.0907 BTU/sec
= 334.18 pounds * 1 BTU/pound-F * 35°F / 7.0907 BTU/sec
= 4,347 seconds
To convert this value to minutes, you can divide it by the number of seconds per minute:
Minutes = dt / seconds/minute
= 4,347 seconds / 60 seconds/minute
= 72.45 minutes
So in this case, dt would equal approximately 72.45 minutes.
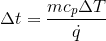
 does not appear in the expression for
does not appear in the expression for  ,
,